Understanding Gradient Learning: A Comprehensive Guide

Gradient learning is a fundamental concept in machine learning and artificial intelligence that has gained significant attention in recent years. This technique is crucial for optimizing algorithms and improving the performance of various models, particularly in deep learning. The essence of gradient learning lies in its ability to minimize the error by adjusting the model parameters in the direction of the steepest descent of the loss function. In this article, we will explore the intricacies of gradient learning, its applications, and its importance in the field of machine learning.

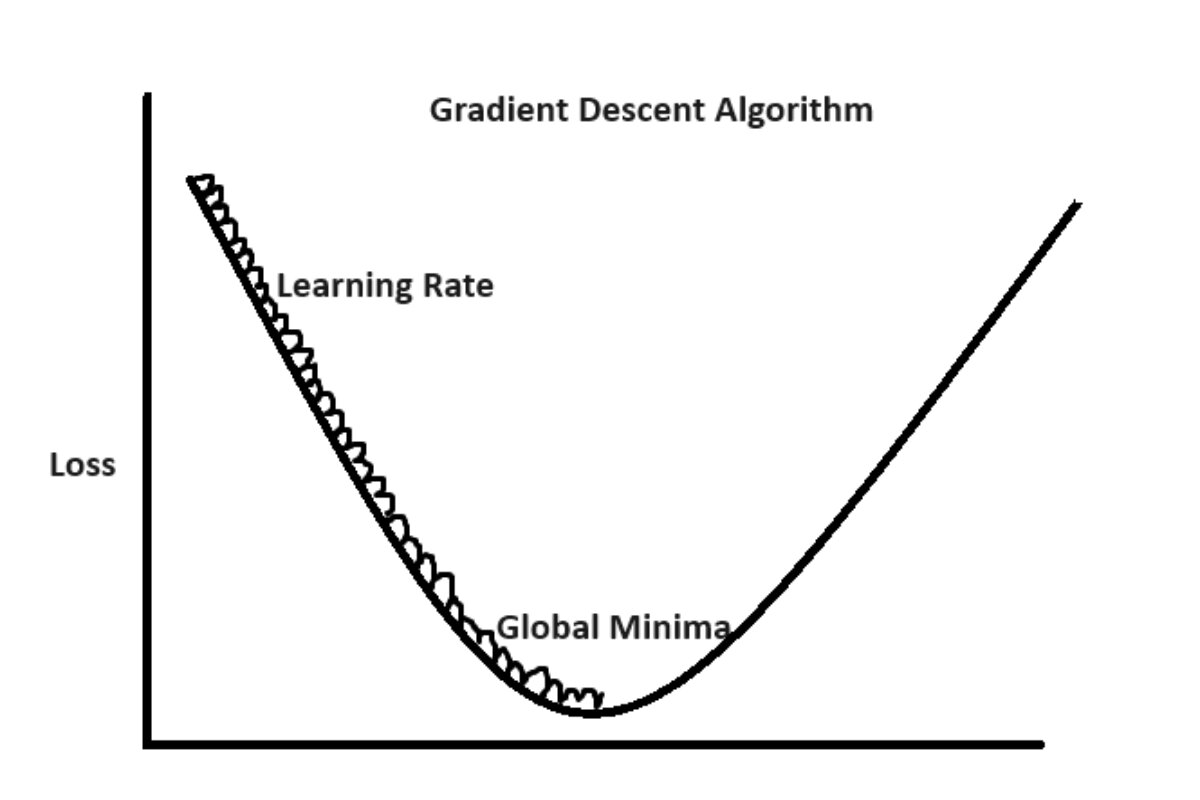
As we delve deeper into the world of gradient learning, it is essential to understand the underlying principles that govern this method. The concept revolves around calculating the gradient of the loss function, which indicates how much the loss would increase or decrease with respect to changes in the model's parameters. By iteratively updating the parameters using this gradient information, we can converge towards an optimal solution that minimizes the error. This process is at the heart of many machine learning algorithms, making it a vital area of study.

In this comprehensive guide, we will cover various aspects of gradient learning, including its definition, mathematical foundations, types of gradient descent, and practical applications. By the end of this article, you will have a solid understanding of gradient learning and its significance in the broader context of machine learning.

Table of Contents

1. Definition of Gradient Learning

Gradient learning refers to the optimization process used in training machine learning models, specifically neural networks. It involves calculating the gradient of the loss function with respect to the model parameters and using this information to update the parameters in a way that minimizes the loss. The primary objective is to improve the model's accuracy and performance by iteratively adjusting the weights based on the gradient information.

2. Mathematical Foundations

The mathematical foundation of gradient learning is rooted in calculus, where the gradient represents the direction and rate of the steepest ascent of a function. In the context of machine learning, we often deal with a loss function, which quantifies the difference between the predicted outputs and the actual outputs.

The gradient of the loss function, denoted as ∇L(θ), is calculated as:

• ∇L(θ) = [∂L/∂θ1, ∂L/∂θ2, ..., ∂L/∂θn]

Where θ represents the model parameters, and L is the loss function. The parameters are updated using the following equation:

• θnew = θold - η∇L(θ)

Here, η (eta) is the learning rate, which controls the step size of each update. A well-chosen learning rate is crucial for effective convergence during the training process.

3. Types of Gradient Descent

Gradient descent is categorized into several types, each with its advantages and disadvantages:

3.1 Stochastic Gradient Descent (SGD)

SGD updates the model parameters using only a single training example at each iteration. This approach can lead to faster convergence but may introduce more noise in the updates.

3.2 Mini-Batch Gradient Descent

This method combines the advantages of both batch and stochastic gradient descent by using a small batch of training examples for each update. Mini-batch gradient descent strikes a balance between convergence speed and stability.

3.3 Batch Gradient Descent

In batch gradient descent, the model parameters are updated using the entire training dataset. While this approach provides a more stable convergence, it can be computationally expensive for large datasets.

4. Applications of Gradient Learning

Gradient learning plays a vital role in various applications across different domains:

• Image Recognition: Used in training convolutional neural networks (CNNs) for object detection and image classification.
• Natural Language Processing: Employed in training recurrent neural networks (RNNs) for tasks such as sentiment analysis and translation.
• Reinforcement Learning: Utilized in optimizing policies in various environments using gradient-based methods.

5. Advantages of Gradient Learning

Gradient learning offers several benefits that contribute to its widespread adoption in machine learning:

• Efficiency: It allows for faster convergence compared to other optimization methods.
• Scalability: Gradient descent techniques can be applied to large datasets, making them suitable for real-world applications.
• Flexibility: Various adaptations of gradient descent can be tailored for specific problems, enhancing their effectiveness.

6. Challenges in Gradient Learning

Despite its advantages, gradient learning also presents several challenges:

• Choosing the right learning rate: A learning rate that is too high may cause divergence, while a rate that is too low can lead to slow convergence.
• Local minima: The optimization process may converge to a local minimum rather than the global minimum, leading to suboptimal performance.
• Overfitting: If not properly managed, models trained using gradient learning can become overly complex and perform poorly on unseen data.

7. Future of Gradient Learning

The future of gradient learning looks promising, with ongoing research focused on improving optimization techniques. Innovations such as adaptive learning rates and advanced regularization methods are being developed to address existing challenges. Additionally, the integration of gradient learning with emerging technologies like quantum computing may revolutionize the field of machine learning.

8. Conclusion

In conclusion, gradient learning is a pivotal concept in the realm of machine learning that facilitates the optimization of algorithms and models. By understanding its principles, mathematical foundations, and practical applications, we can harness the power of gradient learning to build more accurate and efficient machine learning systems. As this field continues to evolve, staying informed about the latest developments in gradient learning will be essential for practitioners and researchers alike.

We encourage you to share your thoughts on gradient learning and its applications in the comments section below. If you found this article helpful, consider sharing it with others who may benefit from it or exploring more articles on our site!

Thank you for reading, and we look forward to seeing you back for more insightful content!

Also Read

Article Recommendations

ncG1vNJzZmivp6x7tMHRr6CvmZynsrS71KuanqtemLyue9WiqZqko6q9pr7SrZirq2dktLOtw6Kcp6xdobKivs2ipaBmmKm6rQ%3D%3D