Understanding Their Differences And Applications

Publish date: 2024-11-29

The t-test is a fundamental statistical tool used in various research fields to determine if there are significant differences between the means of two groups. In this article, we will delve into the differences between paired and unpaired t-tests, helping you understand when to use each type effectively. Grasping the nuances of these tests is crucial for accurate data analysis and interpretation, especially in research that impacts decision-making processes.

Whether you are a researcher, a student, or just someone interested in statistics, understanding the paired vs unpaired t-test can enhance your analytical skills. This comprehensive guide will cover definitions, applications, assumptions, and the steps to conduct these tests. Moreover, we will provide practical examples to illustrate their uses in real-world scenarios.

By the end of this article, you will have a solid understanding of paired and unpaired t-tests, empowering you to make informed choices in your statistical analyses. Let’s dive into the world of t-tests and explore their significance in research.

Table of Contents

1. Definition of T-Tests

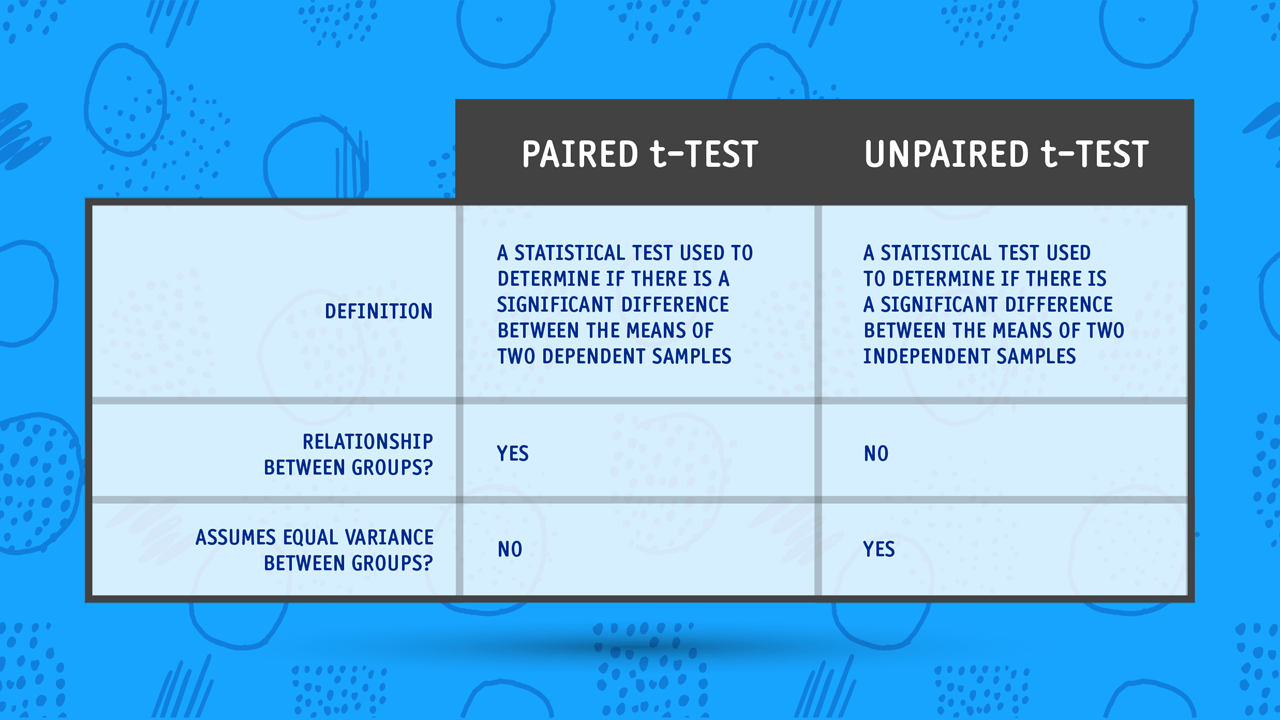
A t-test is a statistical test used to compare the means of two groups and determine if they are significantly different from each other. It helps researchers make inferences about population means based on sample data. The t-test is particularly useful when dealing with small sample sizes, typically less than 30.

2. What is a Paired T-Test?

A paired t-test, also known as a dependent t-test, is used when there are two measurements taken on the same group or individual. This test assesses whether the mean difference between paired observations is significantly different from zero. Common scenarios for employing a paired t-test include:

2.1 Key Characteristics of Paired T-Test

3. What is an Unpaired T-Test?

An unpaired t-test, also known as an independent t-test, is used to compare the means of two independent groups. It assesses whether the mean difference between two separate groups is statistically significant. Scenarios for using an unpaired t-test include:

3.1 Key Characteristics of Unpaired T-Test

4. Assumptions of T-Tests

Both paired and unpaired t-tests have specific assumptions that must be met for the results to be valid:

5. Applications of Paired and Unpaired T-Tests

Understanding when to use paired vs unpaired t-tests is essential in research. Here are some common applications:

5.1 Applications of Paired T-Test

5.2 Applications of Unpaired T-Test

6. How to Conduct Paired and Unpaired T-Tests

Conducting a t-test involves several steps, including data collection, analysis, and interpretation of results. Here’s a brief overview of each process:

6.1 Steps for Conducting a Paired T-Test

  • Collect paired data from the same subjects.
  • Calculate the differences between each pair of observations.
  • Determine the mean and standard deviation of the differences.
  • Use the formula to calculate the t-statistic:
  • Interpret the results using a t-distribution table.

    • 6.2 Steps for Conducting an Unpaired T-Test

  • Collect independent data from two separate groups.
  • Calculate the means and standard deviations for both groups.
  • Use the formula to compute the t-statistic:
  • Check for equal variances using Levene's test.
  • Interpret the results using a t-distribution table.

    • 7. Real-World Examples

    To illustrate the application of paired and unpaired t-tests, consider the following examples:

    7.1 Example of a Paired T-Test

    Researchers want to determine if a new training program improves employee productivity. They measure productivity before and after the training for the same group of employees. By applying a paired t-test, they can analyze whether the mean difference in productivity is significant.

    7.2 Example of an Unpaired T-Test

    A study is conducted to compare the test scores of two different classes taught using different teaching methods. An unpaired t-test is used to assess whether there is a significant difference in the average scores between the two independent groups.

    8. Conclusion

    In summary, understanding the differences between paired and unpaired t-tests is crucial for anyone involved in data analysis. Paired t-tests are ideal for related groups, while unpaired t-tests apply to independent groups. By following the appropriate methodologies and assumptions, researchers can draw meaningful conclusions from their data.

    We encourage you to apply this knowledge in your future research endeavors. If you found this article helpful, please leave a comment, share it with your peers, or explore more articles on our site to further enhance your statistical understanding.

    Sources

    Also Read

    Article Recommendations





    ncG1vNJzZmivp6x7tMHRr6CvmZynsrS71KuanqtemLyue9KtmKtlpJ64tbvKamhoqJGev6awjK%2BqZq2epa6qvsSdZK1lpJrAtXrHraSl